 BACK
BACK We are not major players in the tilting module world (see rather [Donkin] and references therein), but our work lends itself very well to online viewing. And thus to having a homepage. (If you, a major player, would like to be linked (or for us to house your online contribution) it would be great - let us know.)
We have a reasonably fast implementation of [Soergel]'s procedure for
computing the standard module content of tilting modules. This
implementation generates vast amounts of such data.
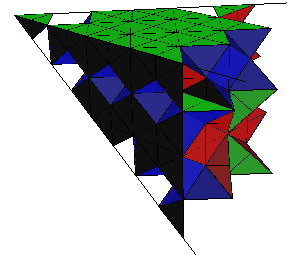
By virtue of the alcove geometric labelling scheme for standard module
weights this data is geometric.
All else being equal, a good way to explore this geometrical data is
to apply alcove geometry to a virtual reality (typically 3D in our
examples).
We animate our viewing of individual tilting modules, and the
iterative procedure.
We do the former so that we may explore the `shape' of the tilting
module in its geometric setting; we do the latter to help search for
patterns of various kinds in the evolution of tilting modules as the
`label' alcove moves away from the fundamental alcove.
Requirements:
To view some `films' of animated tilting modules you need only visit
the library
(under construction, but see
this or
this).
To explore the alcove world in which tilting modules live you need
geomview.
To create your own using our `tilt' package
(Copyright (C) 2000 Paul Martin and Dave Woodcock)
you need a reasonably complete linux, gcc, perl etc.
(see the tarball for details).
Download:
INSTALL:
Assuming you have all the gear,
it is probably enough to go into the tilt/ directory and do
./configure --prefix=WRITE_THE_DIR_NAME_HERE
make bootstrap
make all
./tilt
But see the READMEs too.
CONFIGURATION:
The easiest level of configuration is to use or construct
a type-specific config file called a schematum.
Examples here:
schemata etc,
including user contributed examples.
References and bibliography:
[Donkin] S Donkin, 1993, On tilting modules for algebraic groups,
Math.Z. 212, 39-60.
[Soergel] W Soergel, 1997, Charakterformeln fur Kipp-Moduln uber
Kac-Moody-Algebren, Representation Theory 1, 115-32.
[Lusztig] G Lusztig, 1980, Hecke algebras and Jantzen's generic
decomposition patterns, Adv. in Math. 37, 121-164.
[MartinWoodcock] P P Martin and D Woodcock, 1998, On quantum
spin-chain spectra and the structure of Hecke algebras and q-groups at
roots of unity, J. Phys. A31, 10131-54.
[MartinWoodcock03] P P Martin and D Woodcock, 2003, Generalised
blob algebras and alcove geometry, LMS JCM 6, 249-296.
more
Notes:
Getting tilt to compile under gcc-3.2 required some massaging
cf. the previous version. We havn't yet eliminated all the C++ ISO
non-conforming warnings etc.. It's not compliant, but they're only
warnings.