grad school home     up         |     Introductory notes on partition categories             | WORK IN PROGRESS!!!
Jump (Click me)

Appendix

%\subsubsection{Graphs and pictures} \section{On `Pictures' (of graphs, say) } A `picture' is a device for using the human GPU (cf. references in, say, [Changizi]). In as far as this can be formalised, it incorporates aspects of low-dimensional geometric topology, and some more sophisticated statistical analysis (we will suppress the latter). \subsection{One or two bits of geometric topology} Let $T$ be a topological space and $S$ a subset. Then write $cl(S)$ for the closure of $S$ and write $fr(S) = cl(S) \cap cl(T-S)$.
Recall that a polyhedron is the underlying set of a Euclidean complex.
Theorem. Let $P$ be a polygon (a polyhedron that is the homeomorphic image of a circle) in $\R^2$. Then $\R^2 - P$ has two components.
Theorem (Jordan curve theorem). Let $P$ be the homeomorphic image of a circle in $\R^2$. Then $\R^2 - P$ has two components; and for each component $S$, say, $P=fr(S)$.

These are statements of the `obvious' when one sketches examples, but they are none-the-less central to some of what follows.

By a polygonal arc in $\R^3$ we mean a homeomorphic image of the unit interval in $\R^3$ that is the union of finitely many finite straight-line segments. Such an arc is regular if it is regular in the usual knot theory sense of a polygonal knot in regular position with respect to canonical projection [Crowell-Fox] (with the arc endpoints in particular regarded as vertices).

A pair of polygonal arcs is regular if they may be completed to a regular polygonal arc (possibly by identifying arc endpoint vertices). A finite collection of polygonal arcs is regular if they are pairwise regular and no point in $\R^2$ belongs to the projection image of the interior of more than two arcs.

A collection of polygonal arcs is an embedding of a graph $g=(V,E,f)$ in $\R^3$ if no two arcs meet except possibly at endpoints; and there is a bijection $\Sigma$ from $E$ to the collection of arcs, and an injective map $\Sigma : V \rightarrow \R^3$; such that the endpoints of $\Sigma(e)$ are the images of the corresponding vertex set $f(e)$. An embedding is regular if the collection is regular.

A polygonal line is a subset of $\R^2$ that may be realised as the projection into $\R^2$ of a regular polygonal arc (i.e. of part of a polygonal knot in regular position). A pair of polygonal lines is regular if they may be completed to a polygonal line (possibly by identifying arc endpoint vertices). A finite collection of polygonal lines is regular if they are pairwise regular and no point in $\R^2$ belongs to the interior of more than two lines. 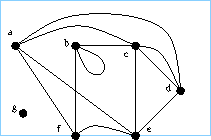\subsection{Graphs and pictures and sketches} It will be useful to represent a graph $g=(V,E,f)$ on a countable vertex set by a `picture' (roughly as in the picture below). This is useful for a number of reasons. Firstly it gives a handy way of representing specific graphs. Secondly it works well with certain ideas of graph composition. Thirdly, it gives a natural way of describing some important special cases, such as planar graphs. However, the use of pictures raises several points of technical difficulty - from the formal to the philosophical. We address some of these here. Our starting point is that people want to (and do) represent graphs using pictures like the one below. How are such pictures to be understood? We address this in two main steps. Firstly, by considering sets constructed in Euclidean geometry that determine graphs; and secondly by considering `models' of such Euclidean geometric constructions that can be realised in the real world. (Just for a moment, we might call the former `pictures' and the latter `sketches' of pictures - but we will soon pragmatically blur the distinction.) %Exercise: %It will be useful to % represent a graph $g$ on a countable vertex set by a picture. A plane drawn picture $(R,S)$ is a closed rectangular interval of the plane $R$ together with a subset $S$ consisting of smoothly embedded line intervals terminating at certain marked points.

The first thing to note is that such a thing can only be approximated by a `drawn picture' (or `sketch') in the artistic sense. Indeed there is nothing in the `physical laboratory' corresponding to a homeomorphic image of a real interval; just as a physical knot or braid is not much like a mathematical knot or braid. However, we will use PDPs in such a way that such approximations are generally sufficient. With this caveat we will speak of `drawing' PDPs, and indeed speak of pictures such as the one on the right as if they are PDPs.

In order to represent a graph $g=(V,E,f)$ by such a picture $(R,S)$, one proceeds as follows. First one draws marked points such that each may be identified with a vertex in $V$. Each edge $\epsilon$ in $E$ is then represented by a line interval between the vertices in $f(\epsilon)$, and labelled by $\epsilon$. There is much freedom of choice in this, but one wants that a complete single line can be determined unambiguously from the drawn set of lines. To this end the set of line interval embeddings is chosen to be
  generic, in the sense that if two lines meet at a point the tangents do not coincide, and no line meets a marked point except at an endpoint.
(This is sophistry, in that it is not really possible to determine tangents to lines by looking at pictures, except within some tolerance. Thus if we use pictures in practice, tangents must not only be different, but sufficiently different.)

In such a picture we shall call the boundary of the rectangular region the frame . A vertex may lie on the frame (call such a vertex exterior), but by convention a line interval may touch the frame only at its endpoints.

An alcove of such a picture $(R,S)$ is a connected component of $R \setminus S$. (See also here.) \subsection{Some `Night thoughts of a ... physicist' on this topic} (`Night thoughts of a classical physicist') The following will not be needed later, but helps to show the risks we take when using physical models of certain constructs in geometry... \subsubsection{Pencil lines and knotted strings} A `curve' is a homeomorphic image of an interval of the real line, typically in $\R^2$. The sense in which a pencil line represents a curve is complicated, and the representation is flawed in several ways. There is no sense in which the atoms in the pencil line form a `linear continuum', even from a classical perspective; and they cannot, in any case, be localised with arbitrary accuracy, on quantum mechanical grounds.

Pencil lines do look like dense linear arrays of points on a number of length scales. And if they looked like such on all length scales then they would be better approximations to `real lines' in the analytical sense. The abstraction of a phenomenon which survives across several length scales to one that survives across all length scales is a very convenient simplification (not only in analysis, but essentially in all modes of human understanding, since, as thinking machines, we are apparently finite). This leaves us with analysis as an abstract tool - but leaves it separated from the real-world phenomena which suggested it. ... \subsection{References} [CF] R H Crowell and R H Fox, Introduction to knot theory, Ginn 1963. [Moise] E E Moise, Geometric topology in dimensions 2 and 3, Springer-Verlag 1977. ...

BACK   NEXT . ...