3d Ising model Partition Function Zeros

P P Martin and Y Valani

This page is under construction.

This model was originally studied in the exact finite lattice approach by Pearson [P82] and Martin [M82,M83] (Martin studied the dual Ising lattice gauge theory), revisited by Bhanot [B95], Valani [V11], and Martin-Valani [MV11]. Unless otherwise stated, results given here can be found in [V11].

Results here are for simple cubic lattices of dimension NxMxL, for various choices of N,M,L.
Boundary conditions:
NxMxL means periodic BCs in every directio.
NxMxL' means peiodic in N,M directions and open BCs in L direction;
and so on. zeros

Table of figures

Figs are plotted in x unless otherwise stated.

4x4x10' (independently computed by two different programs)
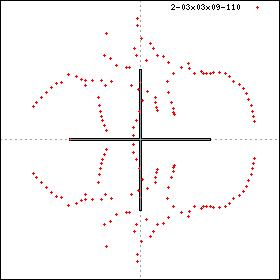
3x3x9'
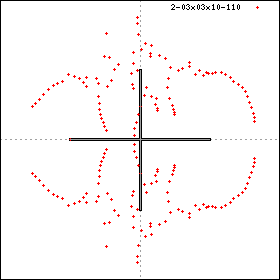
3x3x10'
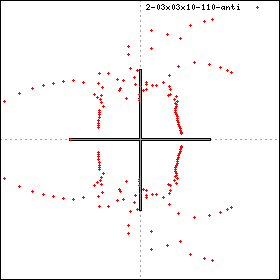
3x3x10' (plotted in 1/x)
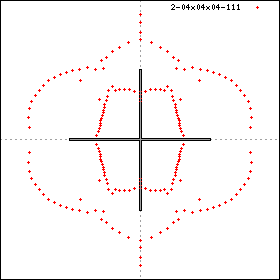
4x4x4

Commentary

Note that with suitable BCs this model has an 8-fold symmetry:
x -> 1/x (unit circle inversion)
x -> -x (imaginary-axis reflection)
x -> x* (real-axis reflection)
With such BCs the zero distribution is determined by the distribution in the first quadrant of the unit disk (or any component of the orbit thereof).
However, many BCs break one or both of the first two symmetries.

If we believe that BCs do not affect the distribution in the large lattice limit (*?) then the departure from symmetry in a finite lattice case gives us a very crude measure of the distance of this lattice size from the limit part of the sequence.
For example, consider the 4x4x10' distribution, which has the inversion symmetry but not the x->-x symmetry. We claim that it is (by eye) relatively left-right symmetrical compared to the 3x3x9' distribution.

The first two results obtained for this model were 4x4x4 [P82] (64 lattice sites) and up to 3x3x9' [M83] (72 lattice sites). The 4x4x4 result exhibits the 8-fold symmetry.
The 3x3x9' result breaks two of these symmetries. In particular 3x3x9' exhibits the property of AF-frustration, meaning that it is not possible to construct a standard checkerboard AF groundstate on such a lattice. In contrast, the trivially ordered Ferromagentic groundstates are present. On this basis one expects the model to be a better approximation to the large lattice limit in the F than the AF region.

With the above remarks in mind we invite the reader to compare the ferro part of the distribution (and that of 3x3x10') with the 4x4x4 case below. To this end we have also plotted 3x3x10' in 1/x. Here the ferro part is in the first quadrant of the unit circle. zeros

Library of zeros data, model by model

1d Ising model, and generalities
2d Ising model -- The control case (via Onsager's solution)
3d Ising model
Q-state Potts models
- 2d, square lattice
  - Q=3
  - Q=4
- 3d
  - Q=3
Clock models

zeros (c) Paul Martin